Conexión Dahlander (V): Solicitud magnética

A pesar de que la solicitud eléctrica en los motores Dahlander se admite que es la misma (generalmente se asume que la corriente que circula por los devanados es la misma independientemente de la configuración que adopte el motor) la solicitud magnética no lo es.

Admitamos la hipótesis simplificativa de que la tensión aplicada a una fase es prácticamente igual a la f.e.m. $$U\cong E = 4.44\cdot\xi \cdot N_s \cdot f \cdot \phi$$ La relación del flujo magnético con la inducción magnética viene dada por la expresión $$\phi=\frac{2\cdot r\cdot l\cdot B}{p}$$ Sustituyendo y reordenando se tiene que la inducción magnétic toma el valor $$U=4.44\cdot\xi\cdot N_s\cdot f\cdot \frac{2\cdot r\cdot l\cdot B}{p} \\ B=\frac{U\cdot p}{4.44\cdot\xi\cdot N_s\cdot f\cdot 2\cdot r\cdot l}$$ Para poder determinar la relación de inducciones magnéticas entre la configuración de baja y alta velocidad será necesario determinar los valores del factor de devanado, $\xi$ y el número de espiras en serie del devanado, $N_s$, para cada configuración.

Es evidente que la estructura de los semidevanados para cada fase es la misma, tanto para la baja como para la alta velocidad, ya que al conmutar los semidevanados lo único que se hace es cambiar la interconexión eléctrica entre ellos y, por tanto, el valor de $r$ y $l$ coinciden.

Sin embargo, los factores de devanado de ambas conexiones no tienen porque tomar el mismo valor.

En efecto, si se toma un devanado Dahlander de dos velocidades (dos y cuatro polos) alojado en un estator de 24 ranuras, se tiene que el ángulo geométrico entre dos ranuras consecutivas es $$\alpha_g=\frac{360}{Nº total ranuras}=\frac{360}{24}=15º$$

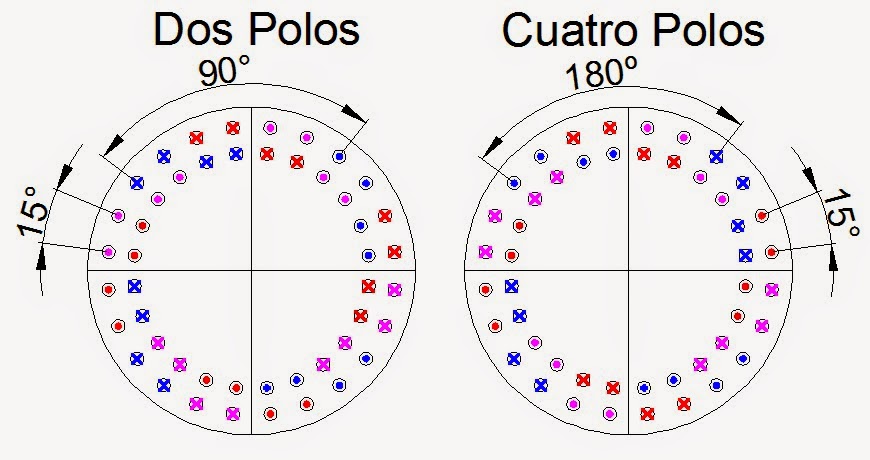Fig. 1

Para la conexión de baja velocidad, 4 polos, y según la distribución del devanado representado en la figura 1, se tiene que cada bobina múltiple del devanado está formada por cuatro bobinas elementales con un ángulo eléctrico entre ellas de $$\alpha_{eB}=p_B\cdot\alpha_g=2\cdot 15=30º$$ La distancia entre la entrada y la salida de una bobina elemental es de 6 ranuras, lo que en grados eléctricos es $$\alpha_{bB}=Nº ranuras\cdot p_B\cdot\alpha_g=6\cdot 2\cdot 15=180º$$ es decir, las bobinas son diametrales cuando el devanado está configurado para la baja velocidad.

Como consecuencia, el factor de devanado, $\xi$, coincidirá con el factor de distribución, $\xi_d$, cuyo valor es $$\xi_B=\xi_{dB}=\frac{\sin{\frac{q\cdot\alpha_{eB}}{2}}}{q\cdot\sin{\frac{\alpha_{eB}}{2}}}=\frac{\sin{\frac{4\cdot\ 30}{2}}}{4\cdot\sin{\frac{30}{2}}}=0.837$$ Para el caso de alta velocidad, el ángulo geométrico entre bobinas sigue siendo el mismo, mientras que el paso polar se ha hecho el doble. Por tanto, la distancia en grados eléctricos entre la entrada y la salida de una bobina elemental es $$\alpha_{bA}=Nº ranuras\cdot p_A\cdot\alpha_g=6\cdot 1\cdot 15=90º$$ es decir, las bobinas del devanado de alta velocidad son de paso acortado $2\cdot\beta_e=90º$.

El factor de devanado es el producto del factor de acortamiento de paso y el factor de distribución $$\xi_a=\xi_{aA}\cdot\xi_{dA}$$ El factor de acortamiento de paso toma el valor de $$\xi_{aA}=\cos{\beta_e}=\cos{45}=\frac{\sqrt{2}}{2}$$ El ángulo eléctrico entre bobinas del devanado de alta velocidad es $$\alpha_{eA}=p_A\cdot\alpha_g=1\cdot 15=15º$$ Luego el factor de distribución tomará el valor de $$\xi_{dA}=\frac{\sin{\frac{q\cdot\alpha_{eA}}{2}}}{q\cdot\sin{\frac{\alpha_{eA}}{2}}}=\frac{\sin{\frac{4\cdot\ 15}{2}}}{4\cdot\sin{\frac{15}{2}}}=0.957$$ Finalmente, el factor de devanado es $$\xi_A=\xi_{aA}\cdot\xi_{dA}=\frac{\sqrt{2}}{2}\cdot 0.957=0.677$$ Una vez calculados los factores de devanado para cada configuración del motor Dahlander, es fácil obtener la relación entre las inducciones magnéticas para cada configuración que toma el devanado.

Conexión a par constante o triángulo-doble estrella (Δ-YY)

Para la conexión a par constante, se tienen las siguientes características para la configuración de baja velocidad $U_B=U$, $N_{sB}=N_s$, $\xi_B=0.837$ y $p_B=2$. Para el devanado de alta velocidad se tiene $U_A=\frac{U}{\sqrt{3}}$, $N_{sA}=\frac{N_s}{2}$, $\xi_A=0.677$ y $p_A=1$.

Finalmente, $$\frac{B_B}{B_A}=\frac{\frac{U_B\cdot p_B}{4.44\cdot\xi_B\cdot N_{sB}\cdot f \cdot 2 \cdot r \cdot l}}{\frac{U_A\cdot p_A}{4.44\cdot\xi_A\cdot N_{sA}\cdot f \cdot 2 \cdot r \cdot l}}=\frac{U_B\cdot p_B \cdot N_{sA}\cdot\xi_A}{U_A\cdot p_A \cdot N_{sB}\cdot\xi_B} \\ \frac{B_B}{B_A}=\frac{U\cdot 2 \cdot \frac{N_s}{2} \cdot 0.677}{\frac{U}{\sqrt{3}}\cdot 1 \cdot N_s \cdot 0.837}=1.4$$

Conexión a potencia constante o doble estrella-triángulo (YY-Δ)

La relación de inducciones magnéticas para la conexión a potencia constante se razona de forma análoga a la ya descrita en el apartado precedente.

En este caso, para la configuración de baja velocidad se tiene $U_B=\frac{U}{\sqrt{3}}$, $N_{sB}=\frac{N_s}{2}$, $\xi_B=0.837$ y $p_B=2$ y para la configuración de alta velocidad $U_A=U$, $N_{sA}=N_s$, $\xi_B=0.677$ y $p_A=1$.

Por tanto la relación entre inducciones magnéticas es $$\frac{B_B}{B_A}=\frac{\frac{U}{\sqrt{3}}\cdot 2 \cdot N_s \cdot 0.677}{U\cdot 1 \cdot 2 \cdot \frac{N_s}{2} \cdot 0.837}=1.87$$

Conexión a par variable o estrella-doble estrella (Y-YY)

Finalmente, el valor de la relación de inducciones magnéticas para la conexión a par variable se obtiene sustituyendo los valores correspondientes para la configuración de baja velocidad $(U_B=\frac{U}{\sqrt{3}}$, $N_{sB}=N_s$, $\xi_B=0.837$, $p_B=2)$ y para la configuración de alta velocidad $(U_A=\frac{U}{\sqrt{3}}$, $N_{sB}=\frac{N_s}{2}$, $\xi_A=0.677$, $p_A=1)$, se tiene $$\frac{B_B}{B_A}=\frac{\frac{U}{\sqrt{3}}\cdot 2 \cdot \frac{N_s}{2} \cdot 0.677}{\frac{U}{\sqrt{3}}\cdot 1 \cdot N_s \cdot 0.837}=0.81$$